How to Solve Sudoku Puzzle
Solution methods and help

Definitions.

A Sudoku puzzle is a grid of 9 x 9 squares, subdivided into 9 regions of 3 x 3 squares. Each square contains one number from 1 to 9. Each row, column and regions of 3 x 3 includes these 9 numbers. Consequently, each row, column and region, when taken individually, cannot contain a number of the same value more than once.

Sudoku Terminology for this website:

A "grid" is a puzzle in the process of being solved or a solved puzzle, or any type of puzzle, as well as an empty puzzle...
A "Sudoku puzzle" is an incomplete grid which contains only one solution.

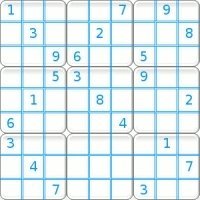A sudoku puzzle	The solution

A "row" is a horizontal line of nine squares.
A "column" is a vertical line of nine squares.
A "region" is a block of 3 x 3 squares.

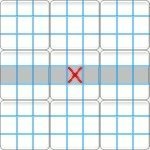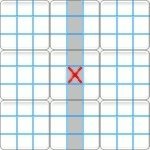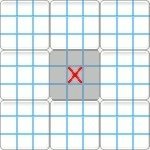Row	Column	Region

A "group" refers to either a row, column or region.

Each square belongs to three different groups. For example, the central square belongs to the following three groups:

	In summary, the three different groups of a square are subject to the same constraints: They each contain the numbers from 1 to 9 which cannot be used more than once.
Three groups

Solution methods.

The following basic methods for solving puzzles are listed below. Other methods shall be added as the software is updated.

There are two principle solution methods.
 • Those puzzles which can be solved directly by using a visual diagram.
 • Those puzzles which can be solved specifically by candidate highlighting.

Candidates of a square refer to the possible numbers that can be entered into that particular square. All of the candidates of a Sudoku puzzle include all the possibilities for all the squares of a grid. The site allows you to display them at any time.

It is advisable, in order to make it easier to solve the puzzle, to start by solving the maximum number of squares visually in order to finish with the minimum number of candidates to be written.

The four basic methods:

Method by inclusion
  • Visually or by reading candidates
Method by exclusion
  • Visually or by reading candidates
Method by exclusive pairs
  • By reading candidates
Multiple choice
  • By reading candidates

Method by Inclusion

One square accepts a number if the three groups of this square have already included eight different numbers. Solutions for this method are those using visual approaches or by studying highlighted candidates.

Visual approach:
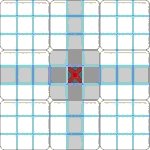
Example: The three groups of the purple square L4C9, already include the eight numbers, in green: 7,2,3,4,6,1,5 and 9. Therefore, 8 is the only solution for this square.

There is no specific visual approach to be applied. Attention should be paid to the squares which have the greatest amount of numbers within them. For example, the gray square L3C4 doesn't prove to be of any interest because there are only two numbers relative to it.

In this grid, a second square uses a solution by inclusion. Can you find it?

Reading the highlighted candidates:
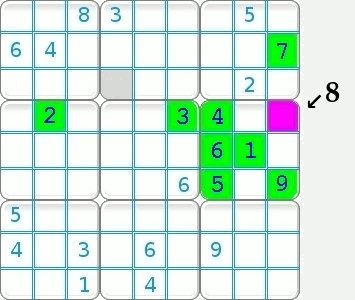
A square having only one possibility naturally uses this possibility as its solution. The purple square L4C9 has only one candidate thereby confirming the visual approach used above.

Have you found the second square?!

In order to practice using this technique, all the beginner level grids found on this site can be solved using the inclusion method.

Method by exclusion

One square accepts a number if this number is excluded from all the other squares of a group pertaining to this particular square. You will notice that a square accepting a solution by exclusion normally has several different possible candidates. Otherwise this square is chosen more simply by inclusion.

This method is solved visually or by studying highlighted candidates.

Three types of cases are possible:
  • Method by exclusion in a region
  • Method by exclusion in a row
  • Method by exclusion in a column

In order to practice using this technique, all the confirmed level puzzles found on this site can be solved using the inclusion and exclusion methods.

Method by exclusion in a region

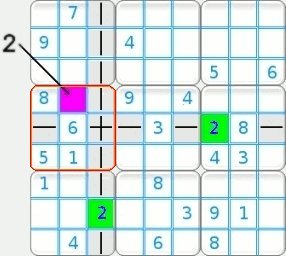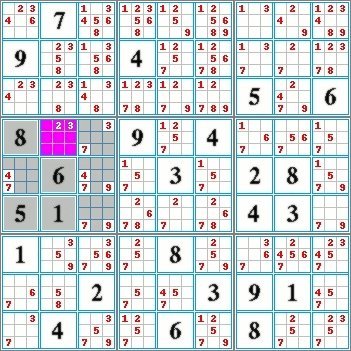Confirmed Level Grid N° 7218: The example, shown on the diagram to the right, indicates how the number 2 is excluded from the orange region, except for the purple cell L4C2. As a result, the purple square is the only cell in this region to accept the 2. This is therefore the solution for this square. The eye must train itself to analyse the numbers in such a way as to project a straight line.

Confirmed Level Grid n° 7218: On the left, seeing the highlighted candidates in the gray region, confirms that the number 2 is only present, in this area, in the purple square L4C2.

In this puzzle, a second square accepts a solution by inclusion. Can you find it? The solution is shown below.

Method by exclusion in a column

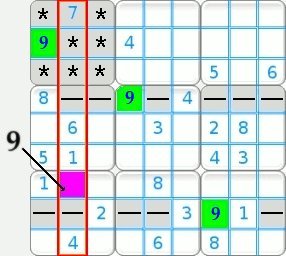Confirmed Level Grid N° 7218: In the example to the left, all the 9's are expelled from the squares of column 2, except those in the purple cell L7C2.: You should also make the habit of looking over the region.

Confirmed Level Grid N° 7218: 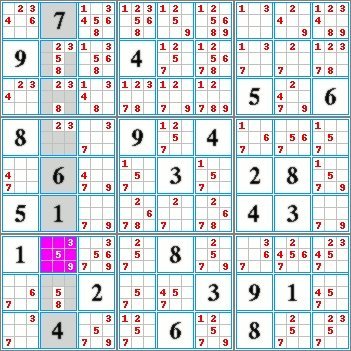To the right, looking at the highlighted candidates in the gray column, the number 9 is only present in this group inside the purple square L7C2.

Method by exclusion in a row

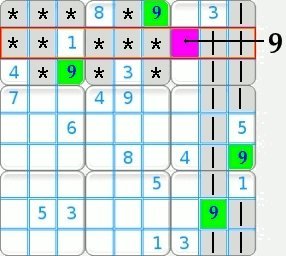Expert Level Grid N° 10000: In the example to the left, all the 9's are expelled from the squares of row 2, except in the purple cell L2C7.Here the eye should look over five zones: The first two regions, the two columns to the right as well as row 2.

Expert Level Grid N° 10000: 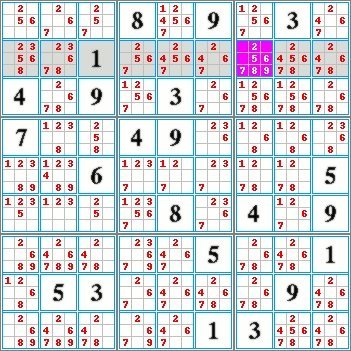To the right, seeing the highlighted candidates in the gray row confirms what is shown on the previous diagram above: the number 9 is only present in this group in the purple cell L2C7. You will notice that the square L2C7 can be solved despite the six possible choices.

Method by exclusive pairs

This method requires the observation of all the highlighted candidates in the grid and involves two guesses.
1st condition: In a group, if two squares contain the same pair of numbers therefore these numbers can be excluded from other squares in this group.
2nd condition: If, following a result of this exclusion, one square is found to have one possible candidate only, then this candidate is the solution for the square.

Two types are possible.
  • Exclusion of a number.
  • Exclusion of two numbers.

Exclusive pair with one number

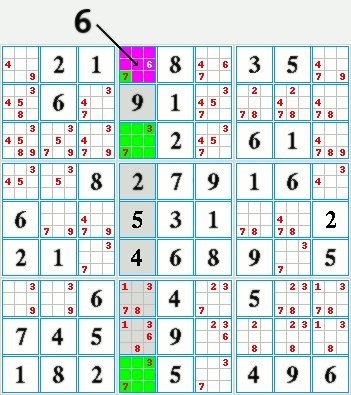Expert Level Grid N° 2616 in the process of being solved. Observe column 4. The two green squares, L3C4 and L9C4 contain the candidates 3 and 7. These are the only two squares in this group to possess this pair of candidates.Therefore, 3 and 7 are naturally the solutions for these two squares. Thus, the purple cell L1C4 excludes the 7. As a consequence the 6 is found to be the only choice for this square. So 6 is the solution for L1C4.

Exclusive pair with two numbers

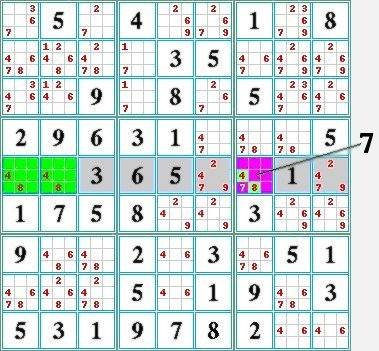Expert Level Grid N° 8131 in the process of being solved. Analyze row 5. The two green squares, L5C1 and L5C2 contain the candidates 4 and 8. They are the only squares in this group to possess this pair of candidates. Therefore, 4 and 8 are the solutions for these two squares. Thus the 4 and the 8 are expelled from the purple square L5C7. Consequently, the 7 becomes the only possibility for this square.So 7 is the solution for L5C7.

Multiple Choice

Multiple choice is not, strictly speaking, a method for solving a square but moreover a lifeline for use as a last resort.
If no square has any solution we choose the one of the square having the least amount of possibilities. We try at random using one of the candidates from this square and attempt to solve the rest of the grid. If we come to a dead end, we retrace our steps backwards to square one having the multiple choice and start over again using another candidate.

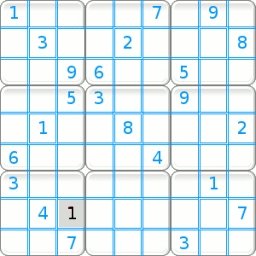The example shown to the left is a puzzle entitled "Al Escargot". To this day it is known as the most difficult Sudoku puzzle to solve. The given numbers of the puzzle are shown in blue. The gray square L8C3 is the first square accepting a solution, the number 1, by exclusion. From this situation, observe the grid listed below which includes the possible candidates.

It appears as though there is no method which can be used for solving the squares for this problem. 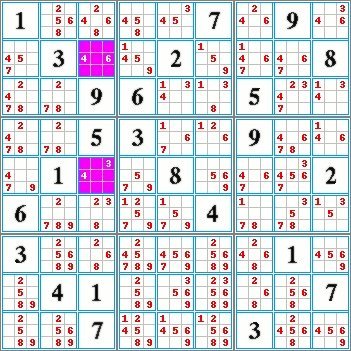It turns out in this case that it is necessary to take at random one of the candidates of one of the squares having the least number of candidates possible. Here it is the 4 or the 6 in L2C3, otherwise the 3 or the 4 in L5C3. If someone has found a method for solving one of the squares present here, please write to us. We will cite this technique with pleasure on the site.

Solution methods not yet exploited by the site

The x-exclusives. Includes all those like exclusive pairs, triplets, quadruple exclusives etc...

Crossed solutions or solutions called level "x".
A pair or one x-exclusive can delete some of the candidates in a square "a" without actually solving it. That may, however, result in solving another square "b" connected with square "a" previously simplified...